偏微分方程在物理学中的完美应用——热方程，推导和示例

作者：老胡

偏微分方程是一个将具有一个以上变量的函数与其偏导数联系起来的方程。为了引入偏微分方程，我们要解决一个简单的问题：模拟薄金属棒内的温度作为位置和时间的函数。在此过程中，我们将从物理原理推导出一维热方程，并求解一些简单的条件：

在这个方程中，温度T是位置x和时间t的函数，k、ρ和c分别是金属的热导率、密度和比热容，称为扩散系数。

我们想要研究，随着时间的增加，热量如何在长为L的金属棒中传导的。

金属棒的一端在处，另一端在处。金属棒的长度远大于它的截面半径，所以我们可以把热传导看成是x和t的函数。

假设金属棒的比热容是已知的，如果我们能找到温度的函数，我们就能知道热量是如何扩散的。

假设棒沿其长度方向是绝热的，因此它只能通过两端吸收或散发热量。这意味着温度分布只取决于以下三个因素：

●初始温度分布情况，这叫做初始条件。

●金属棒两端的温度，和这些叫做边界条件。

●热量在金属棒内由一点传递到另一点的规律。热方程是这种物理定律的数学表示。

对于一组特定的初始和边界条件，求解偏微分方程的问题被称为初始边值问题。

在本文中，我们将求解的热方程的初始边值为。这些叫做齐次边界条件。

热方程可以从能量守恒导出：金属杆上某一点储存的热量的时间变化率等于进入该点的净热量流量。这个过程显然符合连续性方程。如果Q是各点处的热量，V是热量流动的矢量场，则：

根据热力学第二定律，如果两个相同的物体进行热接触，其中一个比另一个热，那么热量必然以与温度差成比例的速度从较热的物体流向较冷的物体。因此，V与温度的负梯度成正比，所以，其中k为金属的导热系数。在一维中，它简化为，其中是方向的单位向量。，代入V和Q的表达式，得到热方程：

，

。

在我们进一步讨论之前，我们需要证明对于任何有物理意义的初始和边界条件，热方程必须存在一个唯一的解。对此的正式证明超出了本文的范围，因此我们将使用一个经验论证。

热力学定律告诉我们，无论一开始金属棒的温度分布是怎样的，系统必须经历一个过程，使金属棒达到热平衡，我们在前面讲过这个过程必须服从热方程，因此，对于有物理意义的初始和边界条件，热方程的解是存在的。此外，经典物理学的基本假设之一是，相同的实验条件必然会导致相同的结果，因此，金属棒进入热平衡的特定方式，由初始条件和边界条件所唯一规定。

这意味着，对于热方程，如果和是两个不同的函数且满足相同的，那么和有相同的形式。此外，热方程是线性的，因此如果和是解，和是任何实数，那么也是一个解。所以我们可以得出结论，解是相同形式的函数的线性组合。

考虑下面的函数，我们可以通过试错来推测：

其中n是大于0的正整数。该??数满足热方程：

。

，

。

这个函数也满足边界条件，因为。因此通解为：

如果我们能找到系数，使这个通解满足初始条件，问题就解决了。也就是说，我们需要找到一个，这样：

这叫做初始条件下的傅里叶正??级数展开式。系数叫做傅里叶系数。

初始条件是区间上的分段连续函数，且在边界处为零。结果证明具有这些性质的函数集合是加法和标量乘法下的向量空间。我们称这个向量空间为：。

这个向量空间有一个内积。对于，一个可能的内积为：

我们可以通过使用单位向量的点积将其投影到轴上来找到几何向量的分量，单位向量构成了的基。同样，如果我们能为找到一个基，那么我们可以将任何投影到基函数上，以便将f表示为基函数的线性组合。

●求v的分量

对于整数，函数是标准正交的：

因此，我们可以将任意函数f∈表示为基集中函数的线性组合：

线性组合的系数由欧拉积分给出：

作为演示，让我们找到一个单位锯齿脉冲的傅立叶系数：

显然，，因此：

。

傅里叶系数为：

因此，锯齿波的傅里叶级数展开为：

下面的动图展示了，随着项的增加，傅里叶级数如何接近锯齿状（波形）的。

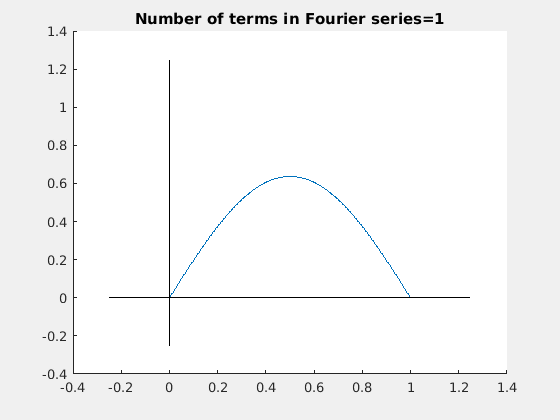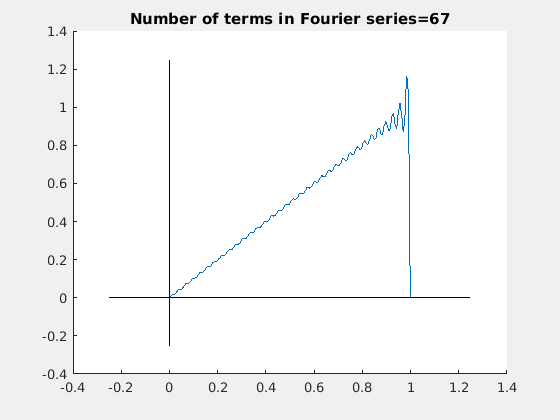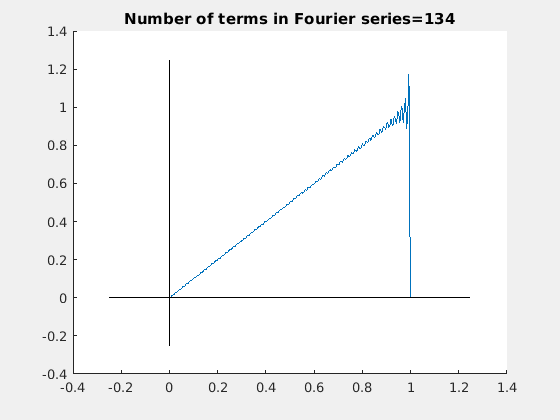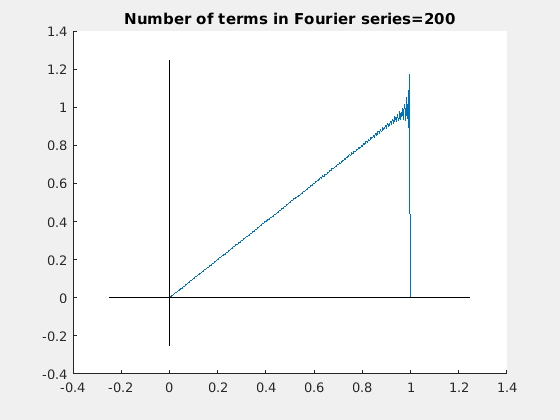
附近的误差称为吉布斯现象。吉布斯现象是一种不可避免的误差，它使不连续函数的傅里叶级数将不连续时的函数值高估约9%。吉布斯现象永远不能完全消除，但当傅里叶级数中的项数接近无穷时，误差收敛到完全局限于不连续点。例如，如果在锯齿形的傅里叶级数展开式中包含无限项，我们会发现当时，级数将完全等于x，而在时，级数的值约为。

这告诉我们，求解热方程的齐次等于使用欧拉积分来求傅里叶系数：

，

，

例：金属棒初始温度是均匀的

假设一个绝热的，一米长的金属棒扩散系数为(不现实，为了方便作图)，最初温度为，在温度为、时夹紧冷却元件。初始条件和边界条件为：

傅里叶系数是：

让我们来验证这个匹配初始和边界条件的傅里叶级数：

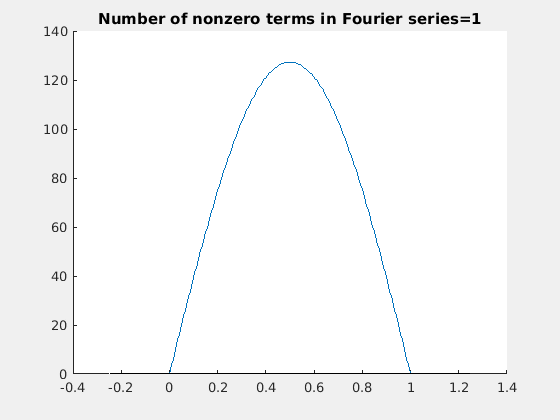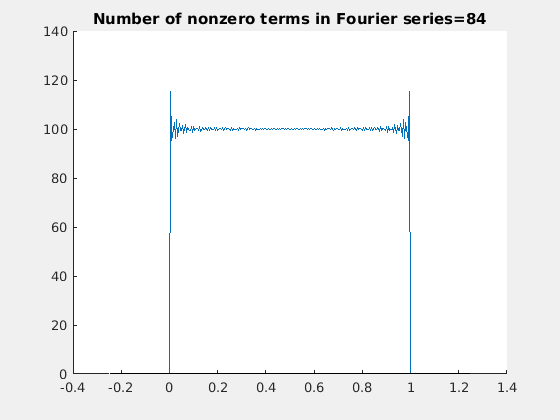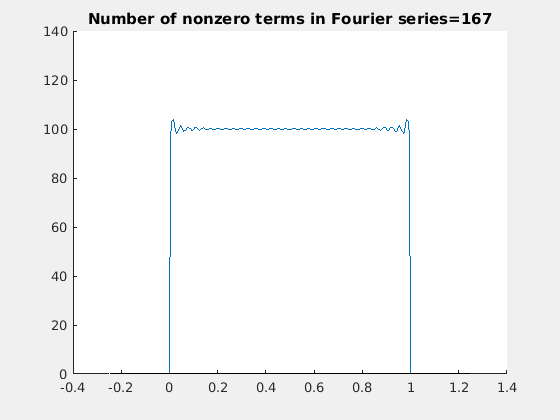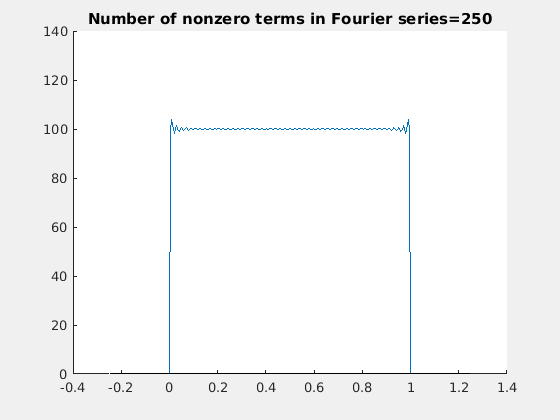
所以，解是：

,

现在让我们画出解：

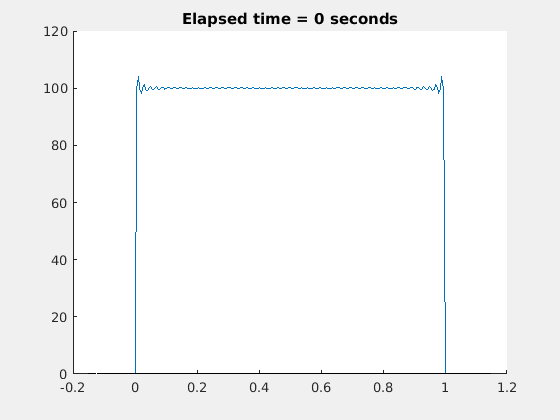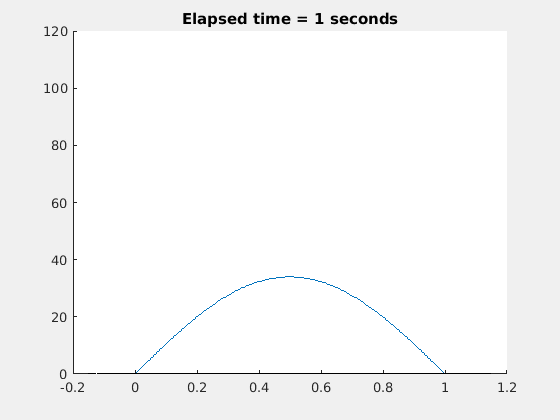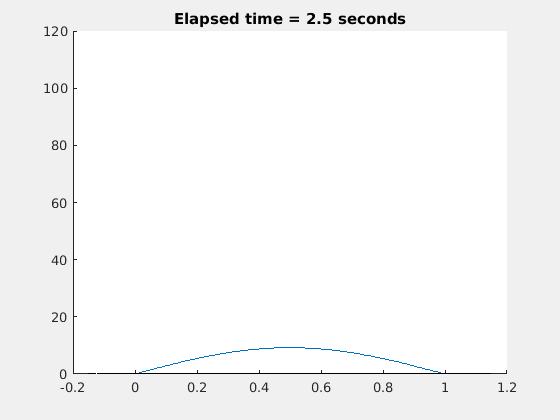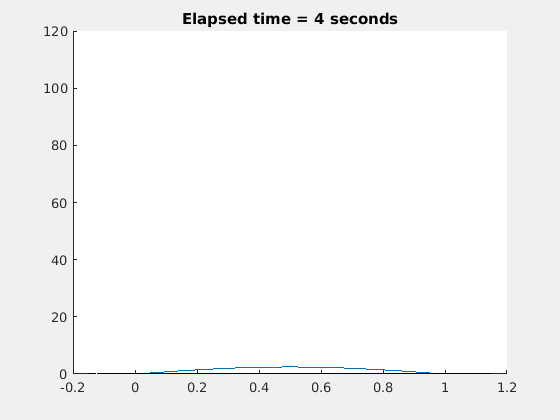
作为一个三维图：

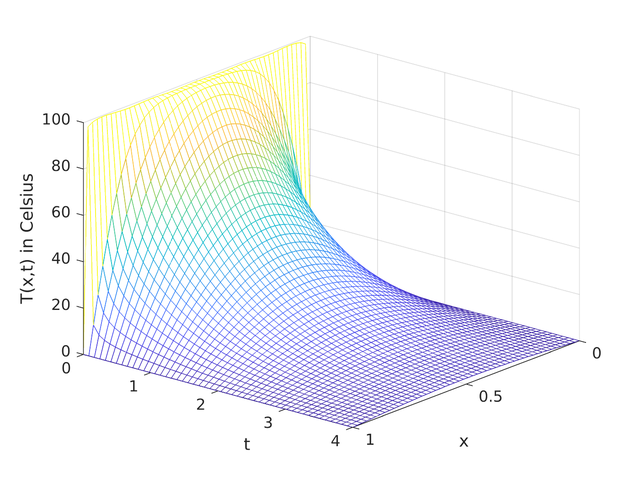
例：温度“尖峰”

现在假设金属棒每个地方的初始温度都是0°C，除了中间10厘米的温度是，这次的扩散系数是。

计算傅里叶系数最简单的方法是把它们转换成更一般的形式：

，，，

所以解是：

，

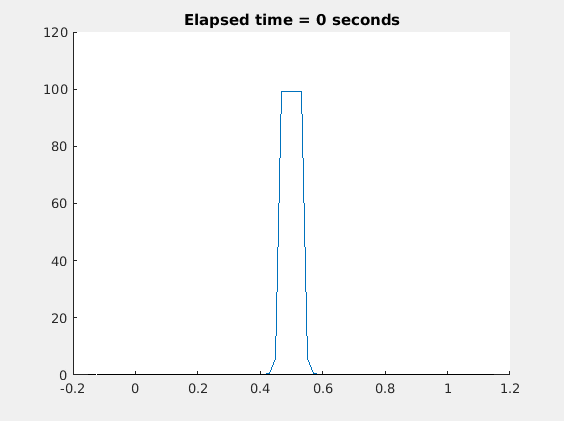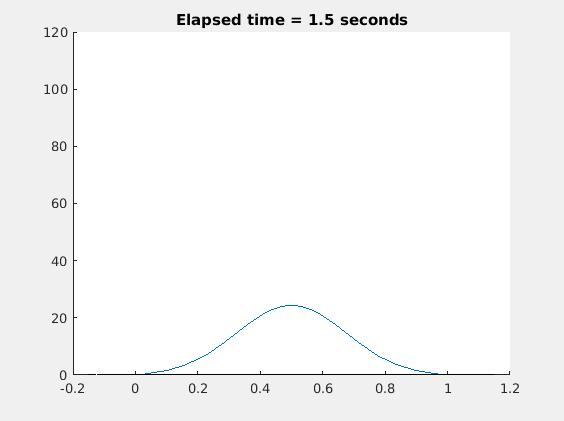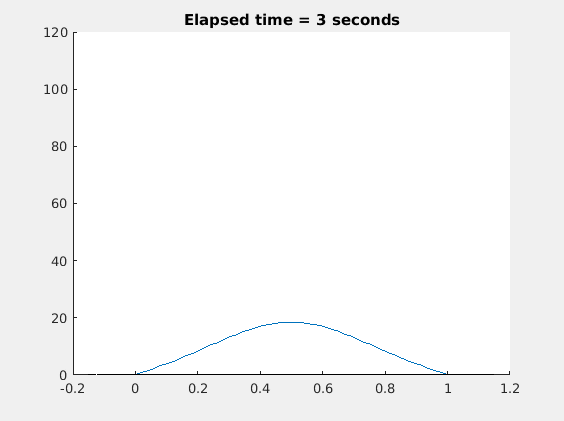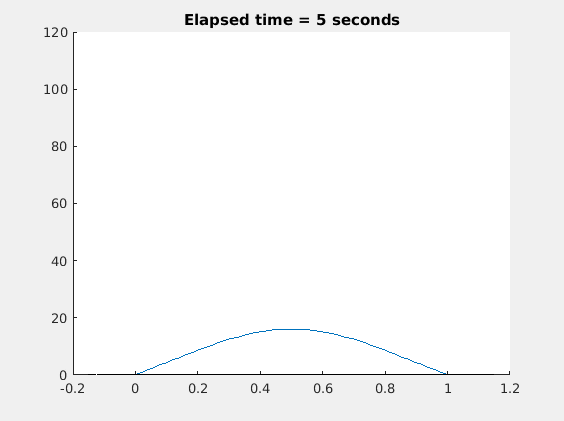
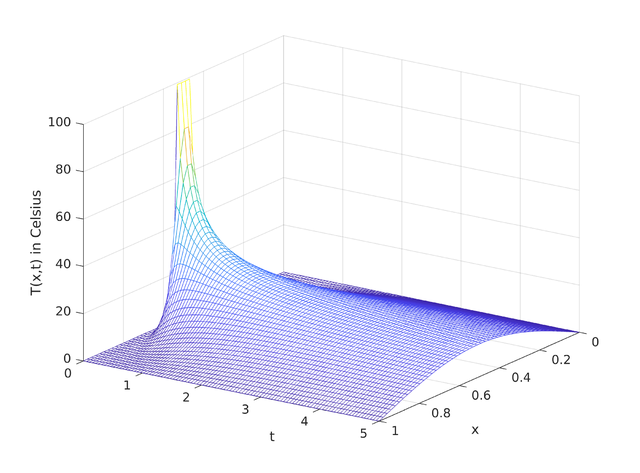
虽然金属棒最终会达到热平衡状态，但是5秒后温度下降的非常缓慢，所以动画值展示5秒。下面是3D图：

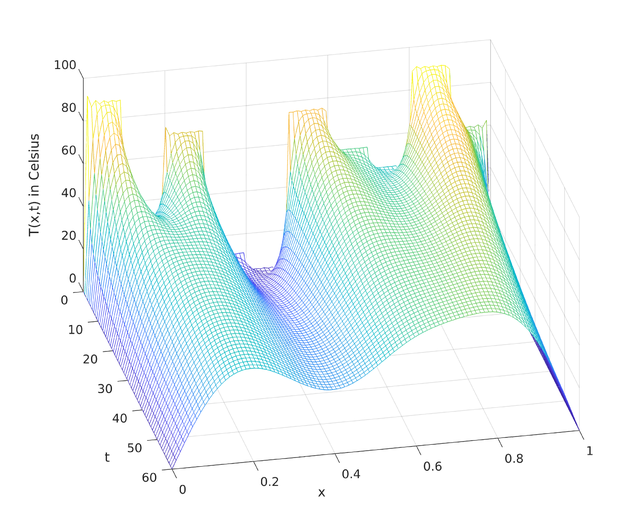
例：随机热分布

这一次，这根金属棒，我们假设是铜做的，扩散系数为，它的热量分布是随机的(以10厘米为一段)，如下表：

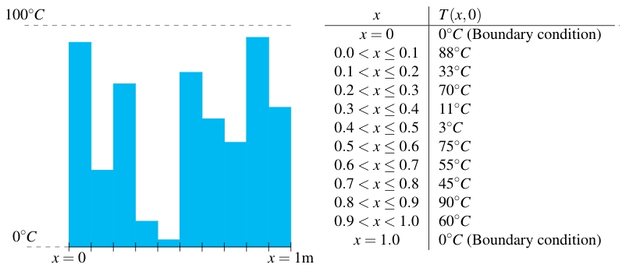
???这种情况下，最好是通过数值积分来求傅里叶系数而不是试图找到一个封闭式的表达式。

下面是一个解的动画：

240秒后，温度的变化非常缓慢。最有趣的行为发生在最初的60秒：

结束语

这就是第一部分的内容。现在你知道了如何解最简单的情况下的热方程，你可以使用热方程来分析更有趣的问题。

想了解更多精彩内容，快来关注老胡说科学。

注：转载本文，仅为展示云章多学科编辑器在理工科复合内容的编辑排版效果，如有异议可致电删除。